[Algorithms] LeetCode 812. Largest Triangle Area
You have a list of points in the plane. Return the area of the largest triangle that can be formed by any 3 of the points.
비행기 좌표가 찍힌 목록이 있다. 임의의 3개의 점으로 그려질 수 있는 가장 큰 삼각형 면적을 반환해라.
Example:
Input: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
Output: 2
Explanation:
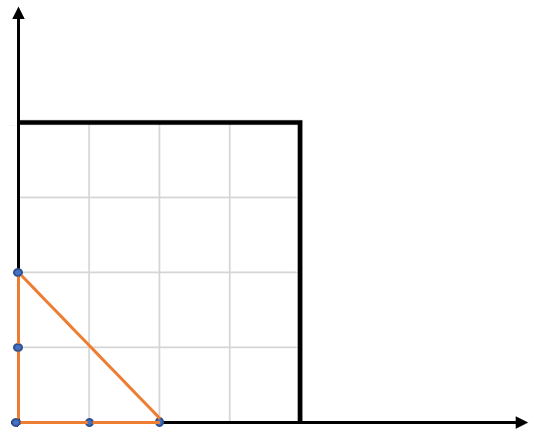
The five points are show in the figure below. The red triangle is the largest.
다섯개 점의 그림은 아래와 같다. 빨간색 삼각형이 가장 크다.
Notes:
3 <= points.length <= 50.- No points will be duplicated.
-50 <= points[i][j] <= 50.- Answers within
10^-6of the true value will be accepted as correct.
Approach #1: Brute Force [Accepted]
Intuition
For each possible triangle, check it’s area and keep the area of the largest.
각각 가능한 삼각형 영역에 대해 면적을 확인하고 가장 큰 면적을 유지한다.
Algorithm
We will have 3 for loops to cycle through each choice of 3 points in the array.
배열의 3개의 점에서 각각의 선택을 순환하기 위해 for 루프 3개를 갖게 된다.
After, we’ll need a function to calculate the area given 3 points. Here we have some options:
이후, 주어진 3점의 면적을 계산하는 함수가 필요하다. 여기에 몇 가지 옵션이 있다.
-
We can use the Shoelace formula directly, which tells us the area given the 3 points;
신발끈 수식을 직접 사용할 수 있다.이 수식은 세 점이 주어진 영역을 알려준다. -
We can use Heron’s formula, which requires the 3 side lengths which we can get by taking the distance of two points;
헤론의 공식을 사용할 수 있다. 헤론의 공식은 두 점의 거리를 취하여 얻을 수 있는 3면의 길이가 필요하다. -
We can use the formula
area = 0.5 * a * b * sin(C)and calculate the angleCwith trigonometry.공식
area = 0.5 * a * b * sin (C)를 사용하여 삼각법으로 각도 C를 계산할 수 있다.
Our implementation illustrates the use of the shoelace formula.
우리의 구현은 신발 끈 수식을 사용한다.
If we did not know the shoelace formula, we could derive it for triangles with the following approach:
신발 끈 수식을 모른다면 다음과 같은 방법으로 삼각형을 도출 할 수 있다.
starting with points (px, py), (qx, qy), (rx, ry), the area of this triangle is the same under a translation by (-rx, -ry), so that the points become (px-rx, py-ry), (qx-rx, qy-ry), (0, 0).
점
(px, py), (qx, qy), (rx, ry)로 시작하면이 삼각형의 면적은(-rx, -ry)에 의한 변환에서 동일하므로 점이(px-rx , py-ry), (qx-rx, qy-ry), (0, 0)이다.
From there, we could draw a square around the triangle with sides touching the coordinate axes, and calculate the area of the square minus the area of the right triangles surrounding the inner triangle.
거기에서 우리는 좌표축을 만지는면이있는 삼각형 주위를 사각형으로 그릴 수 있고, 사각형의 면적에서 내부 삼각형을 둘러싼 직사각형의 면적을 뺀 값을 계산할 수 있다.
For more on this approach, see the Wikipedia entry for the Shoelace formula.
이 접근에 대한 자세한 내용은 신발 끈 수식에 대한 Wikipedia 항목을 참조.
1class Solution {
2 public double largestTriangleArea(int[][] points) {
3 int N = points.length;
4 double ans = 0;
5 for (int i = 0; i < N; ++i)
6 for (int j = i+1; j < N; ++j)
7 for (int k = j+1; k < N; ++k)
8 ans = Math.max(ans, area(points[i], points[j], points[k]));
9 return ans;
10 }
11
12 public double area(int[] P, int[] Q, int[] R) {
13 return 0.5 * Math.abs(P[0]*Q[1] + Q[0]*R[1] + R[0]*P[1]
14 -P[1]*Q[0] - Q[1]*R[0] - R[1]*P[0]);
15 }
16}
1class Solution(object):
2 def largestTriangleArea(self, points):
3 def area(p, q, r):
4 return .5 * abs(p[0]*q[1]+q[0]*r[1]+r[0]*p[1]
5 -p[1]*q[0]-q[1]*r[0]-r[1]*p[0])
6
7 return max(area(*triangle)
8 for triangle in itertools.combinations(points, 3))
Complexity Analysis
- Time Complexity: O(N^3), where N is the length of
points. We use three for-loops of length O(N), and our work calculating the area of a single triangle is O(1). - Space Complexity: O(1).
Soultion : Javascript
Leetcode의 Solution에 소개된 신발 끈 이론을 이용해서 풀었다.
입력값이 let points = [[0,0],[0,1],[1,0]]; 라고 가정하고 풀어본다.
다중 for문을 3중으로 넣어서 모든 배열을 순회하게 할 수 있다.
1for (let p1 of points){
2 for (let p2 of points){
3 for (let p3 of points){
4 }
5 }
6}
신발끈 공식은 삼각형의 넓이를 구할 때 쓰는 공식인데 아래와 같이 함수로 만들 수 있다.
공식에서 x1 = p1[0], x2 = p2[0], x3 = p3[0], y1 = p1[1], y2 = p2[1], y3 = p3[1] 가 된다.
1let shoelace = function(p1, p2, p3) {
2 return 0.5 * Math.abs(p1[0]*p2[1] + p2[0]*p3[1] + p3[0]*p1[1] - p2[0]*p1[1] - p3[0]*p2[1] - p1[0]*p3[1]);
3}
면적은 공식의 결과 값과 앞에 area에 저장된 앞의 넓이 값 중에 큰 값이 면적으로 남는다. 면적의 초깃값은 0으로 설정해둔다.
1let area = 0;
2area = Math.max(area, shoelace(p1, p2, p3));
최종 코드
위 내용을 정리하면 아래와 같다.
1let points = [[0,0],[0,1],[1,0]];
2
3var largestTriangleArea = function(points) {
4 let area = 0;
5 for (let p1 of points){
6 for (let p2 of points){
7 for (let p3 of points){
8 area = Math.max(area, shoelace(p1, p2, p3));
9 }
10 }
11 }
12 return area;
13};
14
15let shoelace = function(p1, p2, p3) {
16 return 0.5 * Math.abs(p1[0]*p2[1] + p2[0]*p3[1] + p3[0]*p1[1] - p2[0]*p1[1] - p3[0]*p2[1] - p1[0]*p3[1]);
17}
중간 결과를 콘솔로그로 출력해보면 이해하기 쉽다.
코드 중간에 출력을 위해 아래 내용을 입력하여 연산되는 값을 확인해본다.
1console.log(`p1[0]:${p1[0]}, p1[1]:${p1[1]}, p2[0]:${p2[0]}, p2[1]:${p2[1]}, p3[0]:${p3[0]}, p3[1]:${p3[1]}`)
2
3console.log(0.5 * Math.abs(p1[0]*p2[1] + p2[0]*p3[1] + p3[0]*p1[1] - p2[0]*p1[1] - p3[0]*p2[1] - p1[0]*p3[1])
1let points = [[0,0],[0,1],[1,0]];
2
3var largestTriangleArea = function(points) {
4 let res = 0;
5 for (let p1 of points)
6 for (let p2 of points)
7 for (let p3 of points)
8 res = Math.max(res, help(p1, p2, p3));
9 return res;
10};
11
12var help = function(p1, p2, p3) {
13 console.log(`p1[0]:${p1[0]}, p1[1]:${p1[1]}, p2[0]:${p2[0]}, p2[1]:${p2[1]}, p3[0]:${p3[0]}, p3[1]:${p3[1]}`)
14 console.log(0.5 * Math.abs(p1[0]*p2[1] + p2[0]*p3[1] + p3[0]*p1[1] - p2[0]*p1[1] - p3[0]*p2[1] - p1[0]*p3[1])
15)
16 return 0.5 * Math.abs(p1[0]*p2[1] + p2[0]*p3[1] + p3[0]*p1[1] - p2[0]*p1[1] - p3[0]*p2[1] - p1[0]*p3[1]);
17}
18
19
20largestTriangleArea(points);
출력 결과 :
for문이 순회하는 것과 각 값이 얼마가 대입되었는지, 면적이 얼마가 구해졌는지 알 수 있다.
1p1[0]:0, p1[1]:0, p2[0]:0, p2[1]:0, p3[0]:0, p3[1]:0
20
3p1[0]:0, p1[1]:0, p2[0]:0, p2[1]:0, p3[0]:0, p3[1]:1
40
5p1[0]:0, p1[1]:0, p2[0]:0, p2[1]:0, p3[0]:1, p3[1]:0
60
7p1[0]:0, p1[1]:0, p2[0]:0, p2[1]:1, p3[0]:0, p3[1]:0
80
9p1[0]:0, p1[1]:0, p2[0]:0, p2[1]:1, p3[0]:0, p3[1]:1
100
11p1[0]:0, p1[1]:0, p2[0]:0, p2[1]:1, p3[0]:1, p3[1]:0
120.5
13p1[0]:0, p1[1]:0, p2[0]:1, p2[1]:0, p3[0]:0, p3[1]:0
140
15p1[0]:0, p1[1]:0, p2[0]:1, p2[1]:0, p3[0]:0, p3[1]:1
160.5
17p1[0]:0, p1[1]:0, p2[0]:1, p2[1]:0, p3[0]:1, p3[1]:0
180
19p1[0]:0, p1[1]:1, p2[0]:0, p2[1]:0, p3[0]:0, p3[1]:0
200
21p1[0]:0, p1[1]:1, p2[0]:0, p2[1]:0, p3[0]:0, p3[1]:1
220
23p1[0]:0, p1[1]:1, p2[0]:0, p2[1]:0, p3[0]:1, p3[1]:0
240.5
25p1[0]:0, p1[1]:1, p2[0]:0, p2[1]:1, p3[0]:0, p3[1]:0
260
27p1[0]:0, p1[1]:1, p2[0]:0, p2[1]:1, p3[0]:0, p3[1]:1
280
29p1[0]:0, p1[1]:1, p2[0]:0, p2[1]:1, p3[0]:1, p3[1]:0
300
31p1[0]:0, p1[1]:1, p2[0]:1, p2[1]:0, p3[0]:0, p3[1]:0
320.5
33p1[0]:0, p1[1]:1, p2[0]:1, p2[1]:0, p3[0]:0, p3[1]:1
340
35p1[0]:0, p1[1]:1, p2[0]:1, p2[1]:0, p3[0]:1, p3[1]:0
360
37p1[0]:1, p1[1]:0, p2[0]:0, p2[1]:0, p3[0]:0, p3[1]:0
380
39p1[0]:1, p1[1]:0, p2[0]:0, p2[1]:0, p3[0]:0, p3[1]:1
400.5
41p1[0]:1, p1[1]:0, p2[0]:0, p2[1]:0, p3[0]:1, p3[1]:0
420
43p1[0]:1, p1[1]:0, p2[0]:0, p2[1]:1, p3[0]:0, p3[1]:0
440.5
45p1[0]:1, p1[1]:0, p2[0]:0, p2[1]:1, p3[0]:0, p3[1]:1
460
47p1[0]:1, p1[1]:0, p2[0]:0, p2[1]:1, p3[0]:1, p3[1]:0
480
49p1[0]:1, p1[1]:0, p2[0]:1, p2[1]:0, p3[0]:0, p3[1]:0
500
51p1[0]:1, p1[1]:0, p2[0]:1, p2[1]:0, p3[0]:0, p3[1]:1
520
53p1[0]:1, p1[1]:0, p2[0]:1, p2[1]:0, p3[0]:1, p3[1]:0
540